Метод моделирования в преподавании физики основной школы

Моделирование, как способ научного познания реальности, давно стало одним из наиболее мощных средств науки. Само слово "модель" было известно очень давно, первоначальное значение слова было связано с архитектурой. В эпоху средневековья оно обозначало масштаб, в котором выражались все пропорции здания. Впоследствии понятием модели стали пользоваться в научных исследованиях, когда непосредственное изучение каких-либо явлений оказывалось невозможным или малоэффективным. Начало моделированию, как методу теоретического исследования, положил И. Ньютон, сформулировав две теоремы о подобии, позволяющие результаты опытов по сопротивлению тел, движущихся в жидкой среде, переносить на другие случаи, в книге "Математические начала натуральной философии".

Метод моделирования имеет большое значение в современных условиях. Он основан на построении соответствующей модели объекта, изучении ее свойств и переносе полученной информации на сам объект. Роль модели состоит в том, что она – заменитель объекта, посредник в отношениях между субъектом и объектом. Под моделью понимается условный образ или образец изучаемого объекта.

В естествознании под физическим моделированием понимается замена изучения некоторого объекта или явления экспериментальным исследованием его модели, имеющей ту же физическую природу.

Так как в Государственном образовательном стандарте предусмотрено изучение методов научного познания в виде отдельного раздела, то необходимо формировать у школьников представление о роли моделирования явлений и объектов, области применения и границ применимости моделей. Бесспорно, это требует перестройки всего учебного процесса в школе так, чтобы учащиеся получили четкое представление о происхождении научных знаний и понимали, как связаны между собой факты, понятия, законы и теоретические выводы.

В курсе физики понятие модели может быть рассмотрено в двух аспектах: модель как объект познания и как средство познания. Проиллюстрируем это. Для рассмотрения понятия модели как объекта познания подходит следующая классификация моделей, в которой все модели делятся на два больших класса: модели материальные и модели идеальные (информационные). А информационные модели в свою очередь делятся на: описательно-информационные, математические (формализованные) и графические.

Рассмотрим возможные примеры моделей взаимодействия двух электрически заряженных тел.

Примером материальной модели такого взаимодействия могут быть крутильные весы Кулона, в которых шарики А и В заряжаются определенным образом и играют роль заряженных тел. А о величине силы взаимодействия между заряженными телами судят по повороту тонкой серебряной упругой нити подвеса.

Описательно-информационная модель: два разноименно заряженных тела притягиваются, а два одноименно заряженных тела отталкиваются, причем сила взаимодействия зависит от расстояния между телами, среды, в которую они помещены и величины заряда тел.

Примером математической модели является связь между величинами в законе Кулона (записанном, например, в скалярной форме в системе СИ): F= k(q1q2/r²)

Графической моделью (рис.1) служит, например, зависимость модуля силы взаимодействия от расстояния между двумя телами (при постоянной величине зарядов тел).

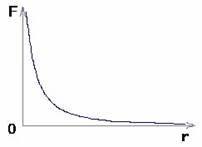
Рис.1

При рассмотрении модели, как средства познания чаще используется деление моделей на материальные (предметные) и теоретические. За редким исключением, любой физический эксперимент – это модель (материальная). А примером теоретической модели может служить модель гармонической электромагнитной волны из курса физики основной школы.

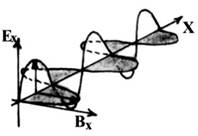
Рис.2

Гармоническая электромагнитная волна (рис.2) – это распространяющееся в пространстве с конечной скоростью гармоническое электромагнитное колебание. Гармоническая электромагнитная волна представляет собой бесконечную синусоидальную волну, в которой все изменения напряженности электрического поля и индукции магнитного поля происходят по закону синуса или косинуса. Причем, колебания вектора напряженности E вектора индукции B в электромагнитной волне происходят перпендикулярно направлению ее распространения. В то же время векторы напряженности и индукции перпендикулярны друг другу. Это означает, что волна движется в направлении, перпендикулярном плоскости, в которой колеблются векторы E и B.