Теорема о соотношении между сторонами и углами треугольника

Эта теорема сформулирована и доказана в учебнике Атанасяна Л.С. [3,с. 68-69], в учебнике Погорелова А.В. такой теоремы нет. Видимо, связанно это с тем, что неравенство треугольника у Атанасяна Л.С. доказывается с использованием выше указанной теоремы. У Погорелова А.В. же неравенство треугольника доказывается с использованием понятия проекции наклонной.

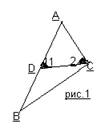
Приведем доказательство теоремы о соотношении между сторонами и углами треугольника дословно.

Теорема: В треугольнике:

1) против большей стороны лежит больший угол;

2) обратно, против большего угла лежит большая сторона.

Доказательство. 1) Пусть в треугольнике АВС сторона АВ больше стороны АС. Докажем, что угол С >угла В. Отложим на стороне АВ отрезок АD, равный стороне АС (рис.1). Так как АD<АВ, то тока D лежит между точками А и В. Следовательно, угол 1 является частью угла С и, значит, угол С >угла 1. Угол 2 – внешний угол треугольника ВDС, поэтому угол 2>угла В. Углы 1 и 2 равны, как углы при основании равнобедренного треугольника АDС. Таким образом, угол С >угла 1, угол 1 = углу 2, угол 2>угла В. Отсюда следует, что угол С >угла В.

2) Пусть в треугольнике АВС угол С >угла В. Докажем, что АВ>АС. Предположим, что это не так. Тогда либо АВ=АС, либо АВ<АС. В первом случае треугольник АВС – равнобедренный и, значит, Угол С= углу В. Во втором случае угол В> угла С (против большей стороны лежит больший угол). И то и другое противоречит условию: угол С >угла В. Поэтому наше предположение неверно, и, следовательно, АВ>АС. Теорема доказана.

Из приведенного доказательства видно, что его идея заключается в проведении дополнительного построения, разбивающего рассматриваемый треугольник на два треугольника, один из которых равнобедренный. Реконструируем идею такого дополнительного построения, доказав эту теорему с использованием понятия о мысленном эксперименте.

Доказательство теоремы с использованием мысленного эксперимента.

Итак, предмет мысли нашего мысленного эксперимента – углы и стороны треугольника. Поместим его мысленно в такие условия (рис.2), в которых его сущность может раскрыться с особой определенностью(1этап).

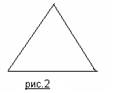
Такими условиями являются:

- равенство всех углов и сторон треугольника (условия равностороннего треугольника);

- способность сторон треугольника «сжиматься» и «растягиваться» сохраняя при этом прямизну линии;

- вершины треугольника могут «скользить» по линиям, содержащим стороны треугольника;

Такие сконструированные условия позволяют нам раскрыть сущность соотношения сторон и углов треугольника с особой определенностью (1 этап) – зависимость величины противолежащего угла от величины противолежащей стороны и обратно.

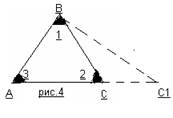
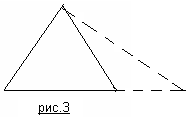
В самом деле, проводя последующие мысленные трансформации (2 этап) путем «растяжения» одной из сторон треугольника (рис.3) мы сможем наблюдать соответственно и увеличение противолежащего угла.

Производя обозначение углов и вершин треугольников (рис.4), получаемых при «растяжении» сторон равностороннего треугольника, мы тем самым мысленно формируем ту среду, ту систему связей, в которую помещаем наш предмет мысли (3 этап).

Увеличивая сторону АС путем «растяжения» до стороны АС1, мы тем самым будем наблюдать увеличение угла 1 и соответственное уменьшение угла 2. Но мы также будем наблюдать увеличение и стороны ВС до стороны ВС1. Если сторона ВС увеличилась больше, чем сторона АС (ВС1>АС1), то теорема не верна. Покажем что это не так.

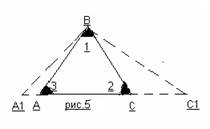
Может быть два случая: ВС1=АС1 и ВС1 ВС1>АС1АС1. В первом случаи треугольник АВС1 был бы равнобедренным, а угол 1 был бы равен углу 3. Но это не так: угол 3 не изменялся и равен 60°, а угол 1 увеличился и стал > 60° – значит стороны ВС1 и АС1 не равны (рис.5). Во втором случае сторону АС1 можно увеличить до стороны ВС1 путем «растяжения» до стороны А1С1 (т.е. А1С1=ВС1) (рис.5). Полученный треугольник А1ВС1 – равнобедренный, а следовательно углы при основании должны быть равны. Но угол 3 уменьшился (т.е. стал < 60°), а угол 1 снова увеличился – значит стороны А1С1 и ВС1 не равны.

Если увеличивать не сторону а угол, мы снова будем решать вопрос о том, какая из двух сторон (АС или ВС) увеличилась больше.

Исходя из проведенного мысленного эксперимента, мы можем заключить истинность утверждения о том, что против большей стороны лежит больший угол и обратно.